Neural Collaborative Filtering 논문 공부

공부한 논문: He, Xiangnan, et al. “Neural collaborative filtering.” Proceedings of the 26th international conference on world wide web. 2017.

recommendation system에 deep learning을 적용하는 방법이야 다양하겠지만, 이 논문은 DNN을 통해 MF의 interaction function을 찾는 방법을 제시했다. 이 논문과 몇몇 참고자료를 바탕으로 내가 공부한 내용을 생각 정리 및 기록용으로 작성해본다.

Recommender system

내가 Recommender System이 되었다고 생각해보자. 내가 해야할 일은 user에게 그가 좋아할만한 item을 추천하는 것이다. 그런데 그 유저가 무엇을 좋아할지 어떻게 알 수 있는가, 혹은 어떻게 정할 것인가? 그냥 인기 많은 걸 추천할 수도 있고(itemPop), 이때까지 user가 좋아해왔던 item과 유사한 특징을 가진 item을 추천할 수도 있다(content-based).
이 논문에서 다루는 것은 Collaborative Filtering(CF)인데, 특정 user와 비슷한 성향의 user군이 좋아했던 item을 추천하는 방식이다. (여러 사람의 데이터가 쓰이는 것이니 이름이 시사하는 바가 확실하다.) 결국 선호도를 수치화해서, 각 user의 각 item에 대한 선호 수준(수치)을 예측해야 하는 문제로 귀결된다.

좀더 자세히 들어가기 전에 CF의 전체적인 메커니즘을 그림으로 살펴보자.

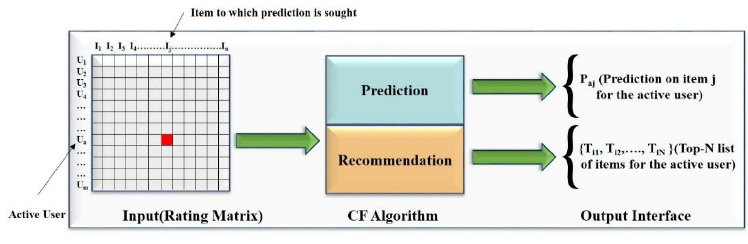Bokde, Dheeraj & Girase, Sheetal & Mukhopadhyay, Debajyoti. (2015). Matrix Factorization Model in Collaborative Filtering Algorithms: A Survey. Procedia Computer Science. 49. 10.1016/j.procs.2015.04.237.

user-item을 표현한 위 matrix에서 관측되지 않은 부분을 예측해야하는데 그 구체적 방법 중 하나가 이 논문에서 다루고, 보완한 Matrix Factorization이다.

preliminaries: learning from implicit data

user-item data는 두 가지로 나눌 수 있는데 하나는 explicit data로 평점 같이 user가 직접 점수화하는 것이다. 다른 하나는 implicit data로, user가 명시적으로 점수화한 데이터는 아니고 우리가 user에게 서비스를 제공하면서 자연적으로 발생하는 data이다. 예를 들어 어떤 비디오 시청을 했다 / 어떤 상품을 샀다 / 어떤 기사를 클릭했다 등이 있겠다. 전자는 noise가 덜하고 더 깨끗한 데이터이지만 모으기가 어렵다.(그런 면에서 사람들이 자발적으로 rating 하게 만든 왓챠는 대단하다) 한편, implicit data는 양적으로 풍부하지만, noise가 심하고 negative feedback 사용이 까다롭다. 어떤 사람이 A비디오를 본 기록이 없다고 하자. 그 비디오가 취향에 맞지 않았던 것일 수도 있지만 그가 아직 존재여부조차 모르는 비디오일 수도 있는 일이다. 이렇듯 interaction이 관측되지 않았다고 무조건 negative로 보기 힘들기 때문에 까다로운 것이다. 이 논문에서는 user-item interaction을 다음과 같이 정의하고 있다.

\[y_{ui} = \begin{cases} 1, & \text{if interaction(user u, item i) is observed} \\ 0, & \text{otherwise} \end{cases}\]

interaction의 예측값을 수식으로 나타내보면 다음과 같다.

\[\hat{y}_{ui} = f(u, i | \theta)\]

NCF의 목표는 \(y_{ui} \)와 가장 가까운 \(\hat{y}_{ui} \)를 산출하는 parameters \(\theta\)를 찾는 것이다.

preliminaries: matrix factorization

MF는 CF의 구체적인 방법으로, 말 그대로 원래 user-item matrix를 분해한다. MF 결과 나온 matrix가 latent matrix(vector)이다. 역시 그림을 보는 편이 이해가 쉽다.

https://developers.google.com/machine-learning/recommendation/collaborative/matrix

좌측의 user-item matrix를 우측의 4 by 2 matrix, 2 by 4 matrix로 분해했다. \(\approx\)가 시사하듯, 오른쪽 4 by 5 matrix는 원 matrix를 완벽히 재현하지는 못한다. 그러나 좌측 matrix에서 체크되어 있는 항목들이 우측 matrix에서 1에 가까운 숫자들인 것을(한 entry만 제외하고) 확인할 수 있다. 여기서 4 by 2 matrix를 user latent matrix로, 2 by 4 matrix를 movie latent matrix로 볼 수 있다.

일반적으로 MF를 어떻게 하는건지 그 방법이 궁금할텐데 우선 이렇게 되어서 무엇이 좋은가부터 생각해보자. 첫 번째로 차원을 줄인다. 두 번째로 user와 item을 같은 차원의 공간에 표현한다. 예를 들어 위의 원래 matrix에서 슈렉이라는 영화를 표현하려면, 네 사람의 선호에 따라 표현될 수 있으니 네 요소가 필요한 셈인데, 두 요소로 줄여진 것이다. 더욱이 user letent matrix와 item latent matrix의 factor 수를 2로 동일하게 맞추었으므로, user와 item을 같은 차원의 공간 안에 표현할 수 있게 되었다. 그래서 한 영화와 한 사용자가 얼마나 가까운지 확인할 수 있게 되는 것이다.

MF를 어떻게 하는가에 대해서 다시 생각해보면, 일단 생각나는건 Singular Value Decomposition이다. SVD는 matrix를 각각 orthogonal matrix U와 V, 그리고 diagonal matrix S로 분해한다. 그런데, SVD는 missing value가 있을 때 쓰기 어렵다(missing value에 값을 채우는 등, 쓸 방법은 많고 그 또한 연구 주제이다). 그래서 나온 것이 ALS이다. 간단하게 말하자면 각 matrix를 고정해놓고 편미분으로 최적 latent matrix P와 Q를 찾는 방법이다. 여기서는 experiment에서 baseline으로 eALS라고 ALS의 빠른, element-wise version을 쓴다. 어쨌든 SVD든 ALS든 matrix factorization의 방법이라는 것이 중요하다. 이런 기존의 MF에 한계가 있어서 새로운 방법을 제시한 논문이기 때문이다.

limination of MF

종래 matrix factorization의 한계는 interaction function이 inner product, 즉 linear함으로써 생기는 것인데, 논문에서는 저차원의 latent space로 옮기면서 raking loss가 일어나는 경우를 예로 든다. jaccard coefficient 순서로는 s41>s43>s42로, 4는 1-3-2순으로 가까워야 하는데 4를 1에 가장 가깝게 위치시키면 어떻게 해도 3보다 2에 가까워지는 그런 경우 말이다. 저차원으로 옮기며 값이 날아가 발생하는 일이니, latent factor k를 더 큰 수로 바꾸면 되는 문제이지만, 기껏 dimensionality reduction을 하게 되는 의미가 없어진다… 그래서 이 논문에서는 interaction function을 좀더 복잡하게 만들어 더 잘 맵핑하도록 학습시켜서 이 문제를 해결하려고 하는 것이다.

general framework

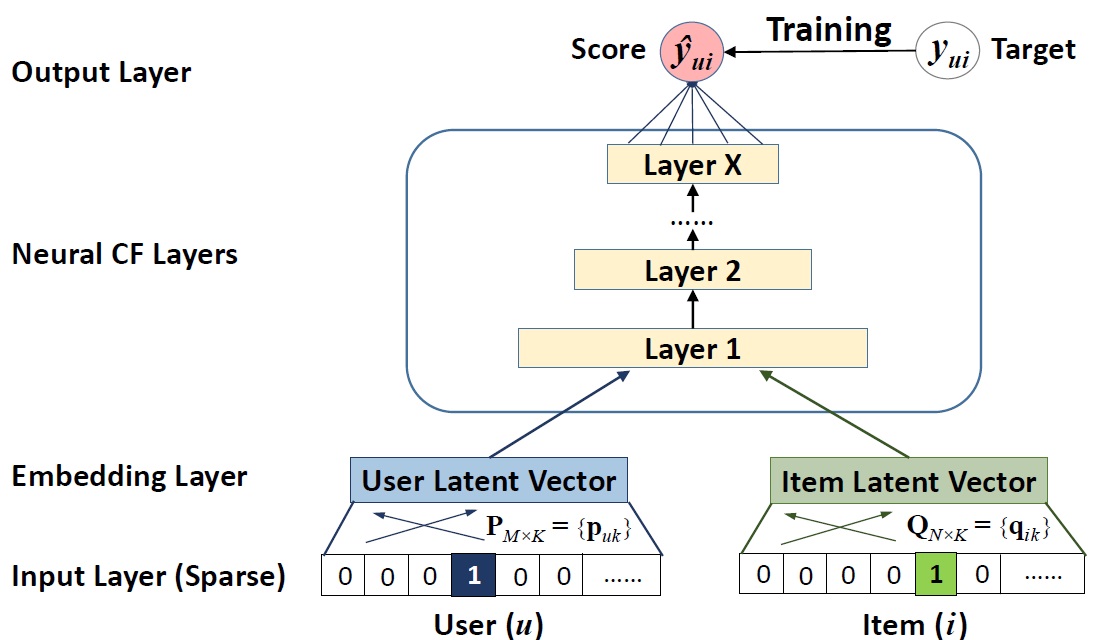He, Xiangnan, et al. “Neural collaborative filtering.” Proceedings of the 26th international conference on world wide web. 2017.
기본적인 NCF 구조

이제 본격적으로 모델을 보자. 간단한 모양이다. input으로 들어가는건 각 user_id와 item_id로 원핫인코딩을 한 sparse matrix이고, 이를 완전히 연결해(fully connected) 두 벡터를 같은 차원으로 임베딩한다(소스보니 keras.embedding을 썼음). 그리고 이 임베딩 레이어가 dnn에 들어가서, dnn에서 matrix에 내재되어 있던 user-item간의 interaction structure를 발견한다. 예측값 \(\hat{y}\)을 수식으로는 다음과 같이 표현할 수 있다.

\[\hat{y}_{ui} = f(u, i | \theta)\]

우리가 자주 보는 weighted least square는 샘플이 가우시안 분포를 따르는걸 전제하는 방법이고, 우리 샘플은 0, 1의 binary한 값을 가지므로 loss function으로 binary cross-entropy를 쓴다. 최적화 방법은 stochastic gradient descent이다.

Generalized Matrix Factorization

그 다음으로는 MF가 NCF의 특수한 케이스라는 것을 보여주려고 한다. NCF에서 hidden layer를 하나 뒀다고 생각하면 \(\hat{y}\)를 다음과 같이 생각할 수 있다.

\[\hat{y}_{ui} = a_{out}(h^T(p_u⊙q_i))\]

여기에서 \(h\)를 uniform vector로 두고 activation function인 \(a_{out}\)을 identity function으로 두면 그냥 MF와 같은 모양을 하고 있다. 이렇게 일반화하려는 이유는, MF를 사용하는 모델이 워낙 많기 때문에 MF가 NCF의 일종이라면 NCF의 확장성도 어느 정도 보장되기 때문인 것 같다. 아무튼 NCF에서는 GMF를 사용할 것이며 \(a_{out}\)으로는 sigmoid function을, \(h\)는 학습되는 값이다! 이로써 latent space에서 factor간 중요성을 달리할 수 있게 되는 것이다.

Multi-layer perceptron(MLP)

non-linearity를 부여를 위해 GMF 말고 다른 버전을 하나 더 생성한다. 바로 MLP를 이용한 방법이다. user-item의 latent vector가 완전 유리되어 생성되기 때문에, 두 개를 concatenating하면서 정보를 합치려는 시도는 직관적이고, multimodal deep learning에서는 흔한 일이다. 그런데 단순 vector concatenating은 user, item latent feature들간 interaction은 전혀 고려하지 않는다. 그렇기 때문에, 벡터를 concatenating하고 standard MLP를 써서 user-item latent features간 작용을 파악하자는 것이다. 활성함수로는 렐루를 쓴다.

NeuMF: Fusion of GMF and MLP

He, Xiangnan, et al. “Neural collaborative filtering.” Proceedings of the 26th international conference on world wide web. 2017.
fused model, NeuMF

실험 결과를 보면 GMF, MLP 버전 둘을 따로 써도 성능이 괜찮지만, 합쳐서 쓰면 아무래도 더 좋을 것이다. 합치기 위해 생각할 수 있는 가장 쉬운 방법은 학습 결과(interaction function)를 combine하는 것이다. 그런데, 그러기 위해서는 같은 사이즈의 embedding vector를 공유해야하는데 그 방법은 모델의 성능을 해칠 수 있다. MLP와 GMF 각각에 최적인 embedding vector의 크기가 다를 수 있기 때문이다. 그래서 각각 다른 embedding을 쓰게 하고, 두 모델의 마지막 은닉층을 합친다. 두 버전을 합친 것이기 때문에, 모델이 복잡해진다. 즉 학습의 결과가 global이 아닌 local에서만 최적인 값이 될 수 있다는 이야기다. pre-train을 하는데 학습에 있어서 초기화가 굉장히 중요하기 때문에, GMF, MLP를 미리 학습시켜놓고 학습 결과 파라미터를 NeuMF에서 처음부터 쓴다. 당연히 결과가 더 좋다.