Examining covid-19 forecasting using spatio-temporal graph neural networks 논문 공부
공부한 논문: Kapoor, Amol, et al. “Examining covid-19 forecasting using spatio-temporal graph neural networks.”
요즘 그래프를 공부하고 있는데 이런 시의적절한, GNN 활용 논문이 있어서 읽어보았다.
Introduction
COVID-19 forecast처럼 전염병 예측의 경우, 접근 방법이 크게 두 가지다. 첫 번째는 mechanistic approach로 전염 역학을 사전적으로 정의한 채 예측하는 방법이다. 두 번째는 time series learning approach다. 시계열 예측에 쓰는 AR이나 시계열 데이터로 LSTM, seq2seq 등 딥러닝을 사용하는 방법이 여기 속한다. 두 approach 모두 상대적으로 inter-regional impact을 (크게) 고려하지 않고, closed-system을 가정하고 있다는 점에서 한계가 있다.
이 논문은 그 한계를 극복하고자 spatio-temporal graph neural network를 이용해 전염의 복합적인 역학을 학습하는 예측 모델을 제안한다.
Background
Spatio-Temporal Graph Neural Networks
spatio-temporal graph는 node간의 연결을 time과 space의 함수로 보는 모델이다. 이 절에서 참조한 논문이 있는데, 해당 논문(Deng, Songgaojun, et al)에서 제안한 모델을 살펴보자.
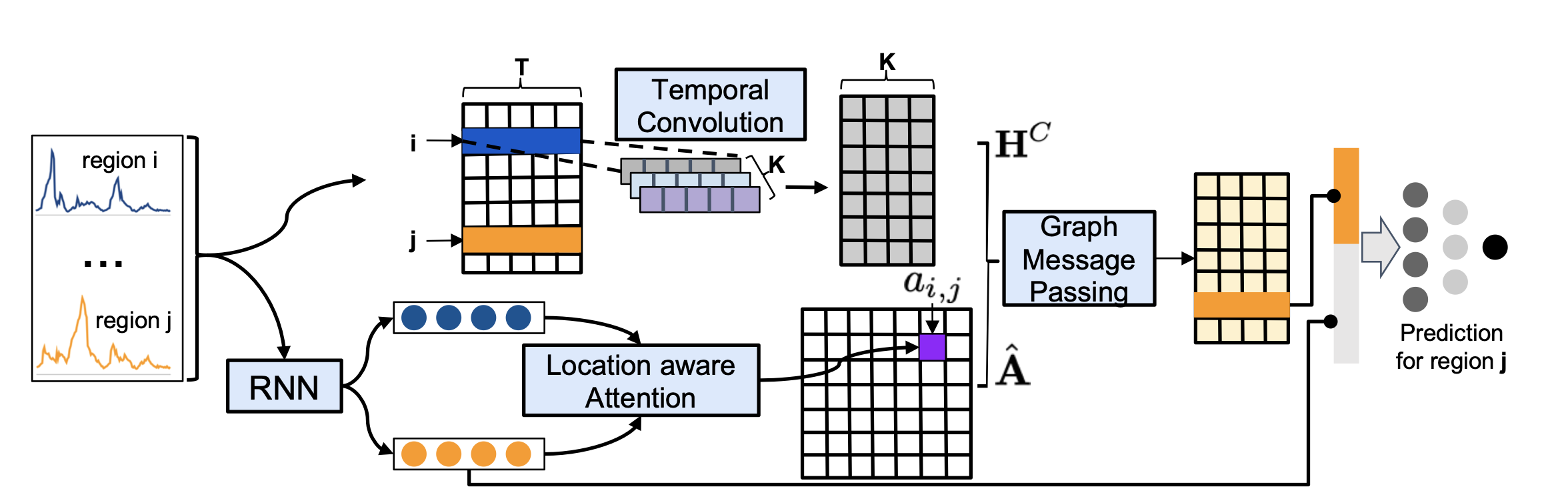
대략 상단이 temporal을, 하단이 spatial을 반영한다.
먼저 spatial 정보를 이용하기 위해 각 region의 t,…,t-d의 sequence를 input으로 하는 RNN을 이용해 t 시점을 재표현한다. 이때 temporal 정보가 좀 반영되는 셈이다. 그리고 그렇게 재표현된 region들의 t 시점 벡터를 이용해 attention coefficient $a_{ij}$를 정의하는데 location i에 location j가 얼마나 영향을 미치는지 나타내게 된다.
다음으로 temporal 정보를 이용하기 위해서, k개의 필터를 이용해 region별로(다시 말해, 한 region의 시계열 데이터를 요소로 하는 벡터) convolution 연산을 한다. convolution 연산을 하기 때문에 region의 temporal sequence가 가진 local pattern을 포착할 수 있다. GNN 모델에서 초기화값, 즉 $h_0$의 노드값으로 이용된다.
다른 논문의 모델이지만, 이 논문 역시 spatial-temporal 모두 이용했다는 점에서 이 논문의 모델을 이해하는데 도움이 되었다.
Method
Graph Neural Networks
일반적인 NN과 마찬가지로 hidden state들을 거치며 가장 마지막 hidden state 뒤에 output이 있다. output은 해결하고자하는 문제에 따라 달라지며 이 경우에는 t+1시점의 case수일 것이다.
GNN의 핵심적인 인사이트는 한 node가 있을 때, 이웃한 node들의 영향을 고려해 임베딩하겠다는 것이다.
message-passing framework에서 l+1번째 layer의 update에 관여하는 요소들은 아래와 같다:
\[m_i^{(l+1)} = \sum_{j\in\mathcal{N}(i)} \mathcal{F}^{(l)}(h_i^{(l)},h_j^{(l)})\] \[h_i^{(l+1)} = \mathcal{G}^{(l)}(h_i^{(l)},m_i^{(l+1)})\]\(h_i^{(l)}\)은 node i의 l번째 hidden state이다. $h_i^{(l)}$에서 $h_i^{(l+1)}$로 업데이트는 두 단계를 거친다.
먼저 주변 노드로부터 message \(m_i^{(l+1)}\)를 얻는다. 이 때 메시지를 얻기 위해 사용하는 function이 \(\mathcal{F}^{(l)}\)이다.
다음으로, 이전에 구한 메시지와 현재 상태를 node update function \(\mathcal{G}^{(l)}\)에 넣어 다음 상태를 구한다.
fuction \(\mathcal{F}^{(l)}\)와 \(\mathcal{G}^{(l)}\)는 학습된다.
Modelling the COVID-19 Graph
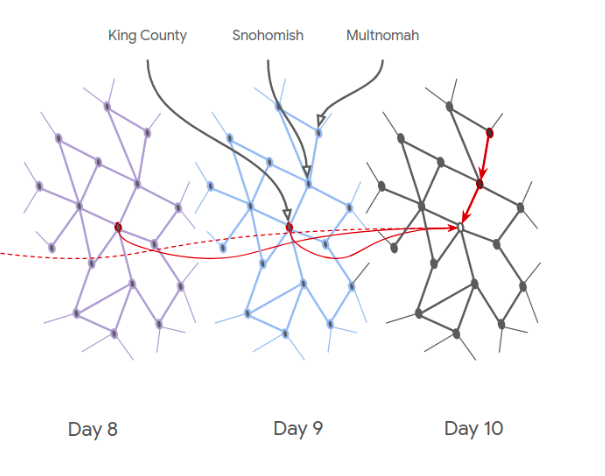
[COVID-19 spatial-temporal graph의 단면]
spatial domain에서는 edge가 intra-flow로 scale된 region간 inter-flow를 나타낸다.
temporal domain에서는 edge는 binary로 연결여부만을 나타내며 t 시점의 node는 t-1, …, t-d 시점의 해당 node와 연결된다.
Skip-Connections Model
\[\mathbf{H}_0 = mlp(x_t|x_{t-1}|...|x_{t-d})\] \[\mathbf{H}_{l+1} = \sigma(\hat{A}H_lW_l) | H_0\] \[\mathbf{P} = mlp(\mathbf{H}_s)\]convolution & skip connection을 활용한 모델이다.
$H_0$은 단순히 node의 temporal 정보를 concatenating해 mlp에 넣은 결과이다.
$H_{l+1}$은 근접행렬(정확히 말하면 어떤 방식으로 정규화된..)과 이전 시점의 hidden state $H_l$, 가중치를 곱하고 그에 $H_0$을 concatenating한다. 즉 근접행렬을 곱하기 때문에 convolution이고 $H_0$을 concat하기 때문에 skip-connection이 되는 것이다.
어떤 l+1의 hidden state에 대해서도 $H_0$이 concat 되기 때문에, 앞에서 살펴봤던 Deng, Songgaojun, et al의 모델에 비해 temporal 정보를 더 강하게 반영하게 되는 것 같다.
끝으로, 제일 마지막 hidden state를 다층 퍼셉트론 모델에 넣어 예측값을 구한다.
그림으로 확인하면 다음과 같다.
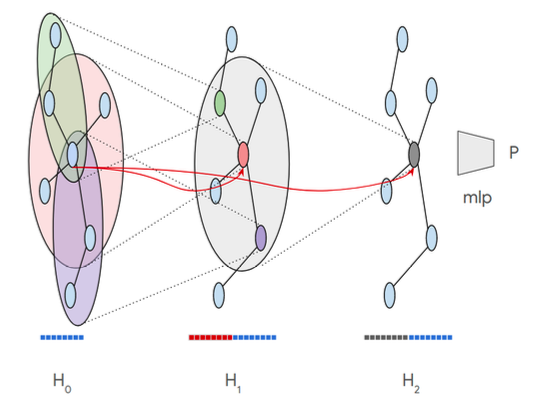
[2-hop skip-connection model]
여기서는 2-hop까지 반영하기 때문에 $H_0$을 제외한 은닉층은 두 개이다.
Experiments
Data
NYT COVID-19 Dataset, Google COVID-19 Aggregated Mobility Research Dataset, Google Community Mobility Reports 데이터를 이용해 데이터를 그래프화하였다. 각 node는 지역정보(state, county)와 날짜, 누적 확진, 누적 사망을 가지고 있다. 앞서 말했듯 edge는 지역간 mobility flow를 나타내는데, Google COVID-19 Aggregated Mobility Research Dataset, Google Community Mobility Reports를 통해 계산되었다.
Case Prediction Performance
RMSLE, Corr을 제시하고 있는데 baseline들보다 대체로 좋게 나왔다. 좀 당황스러웠던 것은, correlation의 경우 현재 시점의 case 수가 바로 이전 시점의 case 수와 같다고 예측한 경우(표의 Previous Cases) 가장 높게 나온 것이다…
Conclusion
전염 역학에 대해 미리 상정하지 않고, 데이터로부터 그 역학을 학습할 수 있다는 점, region level 정보 뿐만 아니라 inter-regional interaction을 적극적으로 반영한다는 점에서 타 모델들과 차별성이 있다.
이 연구는 미국의 county만을 대상으로 하고, 장시간의 데이터로 학습한 것도 아니기 때문에 더 장시간, 넓은 범위를 대상으로 연구하는게 future work가 될 수 있다.
